Présentation

Une EDP parabolique modélise des problèmes de propagation dissipative. Un schéma classique est celui de la diffusion (conduction de la chaleur) :

$$\frac{\partial u}{\partial t} = \frac{\partial^2 u}{\partial x^2}$$

Pour les C.I. 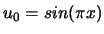$u_0= sin(\pi x)$ et les conditions aux bords 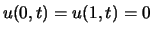$u(0,t) = u(1,t)=0$, on a la solution exacte :

$$u(x,t)=sin(\pi x) e^{-\pi^2 t}$$

remarque : Beaucoup de formes réduites de Navier-Stokes sont gouvernées par des EDP paraboliques.