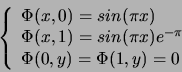Présentation

En mécanique des fluides, les EDP elliptiques sont associées aux problèmes stationnaires. Elles ne modélisent donc plus des problèmes d'évolution comme dans le cas hyperbolique ou parabolique. Les conditions initiales n'ont donc pas la même interprétation (elles deviennent des conditions limites). Une EDP elliptique type est l'équation de Laplace :

$$\frac{\partial^2 \Phi}{\partial x^2} + \frac{\partial^2 \Phi}{\partial y^2} = 0$$

Cette équation gouverne les flux incompressibles à potentiel. Par exemple, pour le domaine $x \in [0,1]$, $y \in [0,1]$ et les conditions aux bords :

$$\left\{ \begin{array}{l} \Phi(x,0) = sin(\pi x) \\ \Phi(x,1... ...n (\pi x) e^{-\pi}\\ \Phi(0,y)=\Phi(1,y)=0 \end{array}\right.$$

La solution est :

$$\Phi(x,y) = sin(\pi x) e^{-\pi y}$$