Forme conservative

Une EDP posée sous forme conservative possède la particularité suivante : Ses coefficients ne se retrouvent pas dans les dérivées.

Par exemple :

	Forme non conservative	Forme conservative
Equ. de continuité $\rho$ et $u$ $=$ $f(x,t)$	$\frac{\partial \rho}{\partial t} + u \frac{\partial \rho}{\partial x} + \rho \frac{\partial u}{\partial x}=0$	$\frac{\partial \rho}{\partial t} + \frac{\partial \rho u}{\partial x} = 0$
Equ. de la chaleur $\rho = \rho (\vec{x})$ $c= c(\vec{x})$ $k=k(\vec{x})$ $T=T(\vec{x},t)$	$\rho c \frac{\partial T}{\partial t} = k \frac{\partial^2 T}{\partial x^2} + \frac{\partial k}{\partial x} . \frac{\partial T}{\partial x}$	$\rho c \frac{\partial T}{\partial t} = \frac{\partial}{\partial x}\Big( k \frac{\partial T}{\partial x} \Big)$

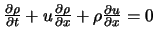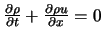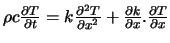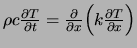Avantages de la forme conservative :

• Meilleure prise en compte des EDP avec coefficients non continus (ex : ondes de choc).
• Prise en compte du principe de conservation sur une région finie. Ceci implique la suppression de petites sources et de petits puits de matière (sauf aux bords du domaine).