On considère ici l'équation de Navier-Stokes en variables primitives (i.e. avec ![]() et
et ![]() comme variables)
sous forme adimensionnelle. L'écoulement est incompressible :
comme variables)
sous forme adimensionnelle. L'écoulement est incompressible :
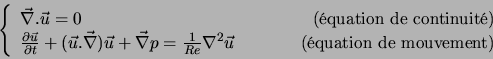
Soit ![]() le domaine et
le domaine et ![]() la frontière. Pour les C.L.,
la frontière. Pour les C.L., ![]() est donné sur
est donné sur ![]() et pour les C.I.,
et pour les C.I.,
![]() est donné sur
est donné sur ![]() sous la contrainte
sous la contrainte
![]() . Il existe une contrainte sur les
C.L. dûe à l'équation de continuité :
. Il existe une contrainte sur les
C.L. dûe à l'équation de continuité :
Cette condition interprète le fait que l'écoulement entrant est égal à l'écoulement sortant à la frontière (conservation
de la masse).
En résolvant l'équation d'évolution de ![]() à
à ![]() , on tombe sur deux problèmes :
, on tombe sur deux problèmes :