



suivant: Système d'EDP d'ordre deux
monter: Systèmes d'équations
précédent: Exemple de système linéarisé
Table des matières
Forme générale :
avec :
On distingue deux types d'EDP d'ordre un dans la direction 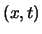 :
:
- Si les valeurs propres de [A] sont réelles et distinctes, le système est hyperbolique dans cette
direction.
- Si les valeurs propres de [A] sont complexes, le système est elliptique dans cette direction.
Pour la direction 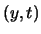 , on observe les v.p. de [B] et on suit le même raisonnement. Par exemple
pour l'équation d'onde :
, on observe les v.p. de [B] et on suit le même raisonnement. Par exemple
pour l'équation d'onde :
donc :
Le comportement est hyperbolique dans la direction 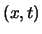
RISSER Laurent
2006-02-04
![\begin{displaymath}
\left\{
\begin{array}{l}
\textrm{[}A\textrm{]} = a_{i,j}(t,...
...connues}\\
\vec{r} = \vec{r}(\vec{u},x,y)
\end{array}\right.
\end{displaymath}](img74.png)
![]() :
:
![]() , on observe les v.p. de [B] et on suit le même raisonnement. Par exemple
pour l'équation d'onde :
, on observe les v.p. de [B] et on suit le même raisonnement. Par exemple
pour l'équation d'onde :
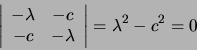
![]()