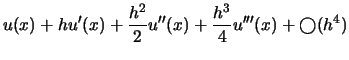 |
(3.1) | ||
 |
(3.2) |
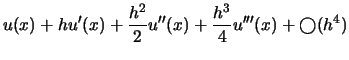 |
(3.1) | ||
 |
(3.2) |
En combinant ![]() et
et ![]() , il vient naturellement :
, il vient naturellement :
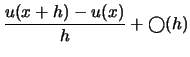 |
(3.3) | ||
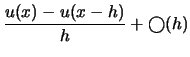 |
(3.4) | ||
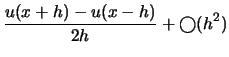 |
(3.5) |
et :
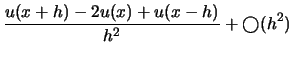 |
(3.6) |
L'équation ![]() est appelée l'approximation à droite de
est appelée l'approximation à droite de ![]() et l'équation
et l'équation ![]() l'approximation à gauche de
l'approximation à gauche de ![]() . Ces deux équations sont cependant grossières
puisqu'elles sont en
. Ces deux équations sont cependant grossières
puisqu'elles sont en ![]() . L'équation
. L'équation ![]() , appelée approximation centrée de
, appelée approximation centrée de
![]() , est plus précise puisqu'elle est en
, est plus précise puisqu'elle est en ![]() . Quand à l'équation
. Quand à l'équation ![]() ,
il s'agit de l'approximation de
,
il s'agit de l'approximation de ![]() et elle est aussi en
et elle est aussi en ![]() .
.
Passons maintenant en dimension deux. On considère maintenant ![]() comme une
fonction de deux variables de classe
comme une
fonction de deux variables de classe ![]() . Le principe d'approximation des dérivées
est exactement le même. Si
. Le principe d'approximation des dérivées
est exactement le même. Si ![]() et
et ![]() tendent vers
tendent vers ![]() , nous avons :
, nous avons :
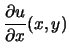 |
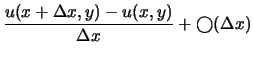 |
(3.7) | |
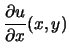 |
 |
(3.8) | |
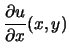 |
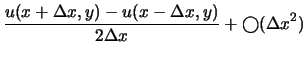 |
(3.9) |
et :
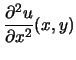 |
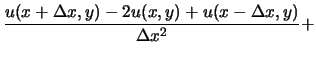 |
||
| (3.10) |
Il en est de même pour les dérivées par rapport à la variable ![]() . Ces formules permettent de comprendre la
discrétisation qui va s'effectuer sur les équations aux dérivées partielles.
. Ces formules permettent de comprendre la
discrétisation qui va s'effectuer sur les équations aux dérivées partielles.