![\begin{displaymath}
\left\{
\begin{array}{lr}
-\frac{d^2}{d x^2} u(x) + p(x) \fr...
... \in ]0,1[\\
u(0) = \alpha\\
u(1) = \beta
\end{array}\right.
\end{displaymath}](img137.png)
Considérons le problème suivant :
![\begin{displaymath}
\left\{
\begin{array}{lr}
-\frac{d^2}{d x^2} u(x) + p(x) \fr...
... \in ]0,1[\\
u(0) = \alpha\\
u(1) = \beta
\end{array}\right.
\end{displaymath}](img137.png)
Nous supposons ![]() ,
, ![]() et
et ![]() suffisement régulières avec
suffisement régulières avec ![]() . Subdivisons le segment
. Subdivisons le segment ![]() en
en
![]() points. Le pas du maillage est :
points. Le pas du maillage est :
Et les noeuds du maillage sont :
Le système est vérifié en chaque point du maillage :
Nous utilisons les approximations ![]() et
et ![]() :
:
On néglige le terme
![]() . En notant
. En notant ![]() la valeur approchée de
la valeur approchée de ![]() aux points
aux points ![]() ,
on obtient :
,
on obtient :
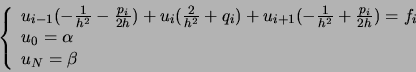
Notons
![]() ,
,
![]() et
et
![]() . Nous
aboutissons alors au système :
. Nous
aboutissons alors au système :
![\begin{displaymath}
\left[
\begin{array}{cccccc}
b_1&c_1&0&&&\\
a_2&b_2&c_2&&&\...
...ts\\
f_{N-2}\\
f_{N-1} - c_{N-1} \beta\\
\end{array}\right]
\end{displaymath}](img154.png)
Il reste à étudier l'ordre du schéma, sa consistance et sa convergence. Nous verrons plus tard dans ce chapitre comment faire.