Stabilité

Ce concept s'applique aux problèmes d'évolution. Par définition, un schéma numérique est stable si les erreurs (d'arrondi, de troncature,...) ne peuvent pas croître pendant la procédure numérique d'un pas de temps au suivant.

Un schéma peut être :

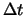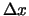• Inconditionnellement stable : Quels que soient $\Delta t$ et $\Delta x$ les erreurs causées par le schéma numérique n'explose pas au fil des itérations.
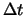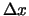• Conditionnellement stable : On doit poser une condition sur $\Delta t$ et $\Delta x$ pour que la solution n'explose pas.
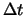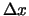• Inconditionnellement instable : Quels que soient $\Delta t$ et $\Delta x$ les erreurs s'amplifient au fil des itérations. Ceci cause des résultats complètement faux.