



suivant: Cas incompressible
monter: Les équations de la
précédent: Les équations de la
Table des matières
Les équations de Navier Stokes compressible sous forme conservatives sont :
avec :
où :
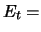 énergie totale par unité de volume
énergie totale par unité de volume
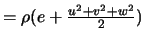
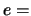 énergie interne par unité de masse
énergie interne par unité de masse
 tension visqueuse (Newtonienne) =
tension visqueuse (Newtonienne) =
![$\mu [( \frac{\partial u_i}{\partial x_j} + \frac{\partial u_j}{\partial x_i}) - \frac{2}{3} \delta_{ij} \frac{\partial u_k}{\partial x_k}] \qquad (i,j,k = 1,2,3)$](img210.png)
-
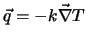 (loi de Fourier)
(loi de Fourier)
-
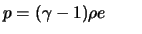 (pour gaz parfait
(pour gaz parfait 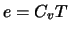 ,
,
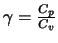 ,
, 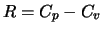 alors
alors 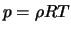 )
)
-
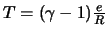
Si on re-écrit ces équations sous forme adimensionnelle avec :
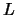 = longueur caractéristique
= longueur caractéristique
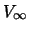 = vitesse caractéristique
= vitesse caractéristique
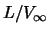 = temps caractéristique
= temps caractéristique
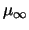 = viscosité dynamique caractéristique
= viscosité dynamique caractéristique
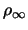 = masse volumique caractéristique
= masse volumique caractéristique
 =
=
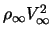 = pression caractéristique
= pression caractéristique
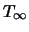 = temps caractéristique
= temps caractéristique
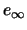 =
= 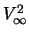 = énergie interne caractéristique
= énergie interne caractéristique
-
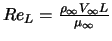 ,
,
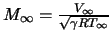 ,
,
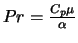 ,
,
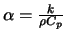
on retouve les mêmes équations avec :
et les équations d'état sont :
La pression a une signification thermodynamique dans le cas compressible.




suivant: Cas incompressible
monter: Les équations de la
précédent: Les équations de la
Table des matières
RISSER Laurent
2006-02-04
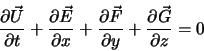
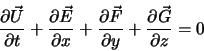
![\begin{displaymath}
\vec{U} =
\left[
\begin{array}{c}
\rho \\
\rho u \\
\rho v\\
\rho w\\
E_t
\end{array}\right]
\end{displaymath}](img202.png)
![\begin{displaymath}
\vec{E} =
\left[
\begin{array}{c}
\rho u \\
\rho u^2+p-\tau...
...\tau_{xx} - v \tau_{xy} - w \tau_{xz} + q_x
\end{array}\right]
\end{displaymath}](img203.png)
![\begin{displaymath}
\vec{F} =
\left[
\begin{array}{c}
\rho v\\
\rho uv - \tau_{...
...\tau_{xy} - v \tau_{yy} - w \tau_{yz} + q_y
\end{array}\right]
\end{displaymath}](img204.png)
![\begin{displaymath}
\vec{G} =
\left[
\begin{array}{c}
\rho w\\
\rho uw - \tau_{...
...\tau_{xz} - v \tau_{yz} - w \tau_{zz} + q_z
\end{array}\right]
\end{displaymath}](img205.png)