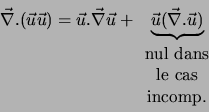Si ![]() est constant en amont alors
est constant en amont alors ![]() est constant partout dans le domaine. Alors :
est constant partout dans le domaine. Alors :
L'équation de Navier-Stokes en variables primitives ![]() est alors (forme non conservative) :
est alors (forme non conservative) :
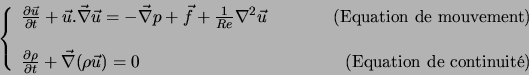
avec :
Ici, la pression a une signification mécanique et non pas thermodynamique. La forme conservative des équations de
N.S. est :
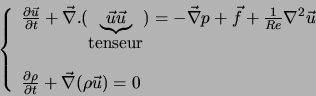
car :