Transformations non singulières

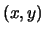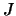Supposons une transformation de $(x,y)$ vers $(\xi,\eta)$ (variables indépendantes) non singulière. $J$ le jacobien de la transformation :

$$J = \frac{\partial (\xi , \eta)}{\partial (x, y)} = \left\v... ..._y \end{array}\right\vert = \xi_x \eta_y - \xi_y \eta_x \neq 0$$

Calcul de l'équation transformée :

• $\Phi_x= \Phi_{\xi} \xi_{x} + \Phi_{\eta} \eta_{x}$
• $\Phi_{xx} = (\Phi_{x})_x = \Phi_{\xi \xi} \xi_x^2 + 2 \Phi_{\xi \eta} \xi_{x} \eta_{x} + \Phi_{\eta \eta} \eta_x^2 + \Phi_{\xi} \xi_{xx} + \Phi_{\eta} \eta_{xx}$
• mêmes calculs pour $\Phi_y$, $\Phi_{yy}$, $\Phi_{xy}$

En remplaçant dans (1), on trouve :

$$A \Phi_{\xi \xi} + B \Phi_{\xi \eta} + C \Phi_{\eta \eta} + \cdots = g_2(\xi , \eta) \qquad \textrm{(2)}$$

avec :

• $A = a \xi_x^2 + b \xi_x \xi_y + c \xi_y^2$
• $B= 2 a \xi_x \eta_x + b \xi_x \eta_y + 2 c \xi_y \eta_y$
• $C= a \eta_x^2 + b \eta_x \eta_y + c \eta_y^2$
  

Le discriminant de (2) est :

$$B^2-4AC = (b^2-4ac)(\xi_x \eta_y - \xi_y \eta_x)^2 = J^2 (b^2 - 4 ac)$$

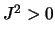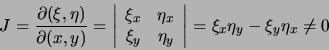
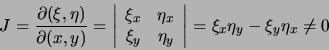
or $J^2>0$ donc l'équation transformée est du même type que l'équation initiale.