



suivant: Transformations non singulières
monter: Rappels sur les Équations
précédent: Rappels sur les Équations
Table des matières
On distingue EDP linéaire et EDP non linéaire. Les EDP linéaires ne contiennent
aucun produit de variable avec elle même ou une de ses dérivées alors que les EDP
linéaires peuvent en posséder. Par exemple :
avec 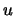 qui dépend de
qui dépend de 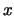 et de
et de 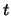 et
et  une constante. Nous nous focalisons ici sur les EDP linéaires.
Les EDP non linéaires seront l'objet d'étude des derniers chapitres de ce cours.
une constante. Nous nous focalisons ici sur les EDP linéaires.
Les EDP non linéaires seront l'objet d'étude des derniers chapitres de ce cours.
La classification des EDP linéaires se fait sur la base d'une équation d'ordre 2 standard :
où 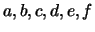 sont fonctions de
sont fonctions de 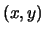 . C'est une équation linéaire.
Le type de l'EDP dépend de son discriminant,
. C'est une équation linéaire.
Le type de l'EDP dépend de son discriminant,
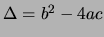 :
:
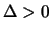 alors, l'EDP est hyperbolique.
alors, l'EDP est hyperbolique.
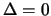 alors, l'EDP est parabolique.
alors, l'EDP est parabolique.
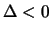 alors, l'EDP est elliptique.
alors, l'EDP est elliptique.
Sous-sections
RISSER Laurent
2006-02-04


![]() qui dépend de
qui dépend de ![]() et de
et de ![]() et
et ![]() une constante. Nous nous focalisons ici sur les EDP linéaires.
Les EDP non linéaires seront l'objet d'étude des derniers chapitres de ce cours.
une constante. Nous nous focalisons ici sur les EDP linéaires.
Les EDP non linéaires seront l'objet d'étude des derniers chapitres de ce cours.
![]() sont fonctions de
sont fonctions de ![]() . C'est une équation linéaire.
Le type de l'EDP dépend de son discriminant,
. C'est une équation linéaire.
Le type de l'EDP dépend de son discriminant,
![]() :
: