



suivant: Domaine borné
monter: EDP hyperboliques
précédent: Présentation
Table des matières
Une caractéristique interprète la vitesse et direction à laquelle est transportée l'information au
cours du temps.
Pour une équation :
on cherche les
coordonnées caractéristiques  et
et 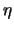 telles que
telles que
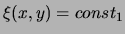 et
et
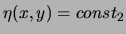 le long de
ces carctéristiques. Pour (3), on a
le long de
ces carctéristiques. Pour (3), on a
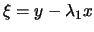 et
et
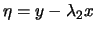 avec :
avec :
Par exemple :
Cette équation régit la propagation d'une onde sonore à vitesse 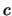 en milieu uniforme dans
le temps et l'espace. Les courbes caractéristiques de ce problème sont les courbes intégrales de :
en milieu uniforme dans
le temps et l'espace. Les courbes caractéristiques de ce problème sont les courbes intégrales de :
On dit que l'information se propage le long des caractéristiques. (ie : en prenant comme C.I. un Dirac
en 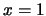 et
et 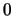 ailleur, on va observer son déplacement le long des caractéristiques)
ailleur, on va observer son déplacement le long des caractéristiques)
RISSER Laurent
2006-02-04
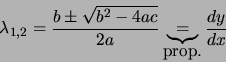
![\begin{displaymath}
\left\{
\begin{array}{l}
\frac{\partial^2 u}{\partial t^2} =...
... [- \infty , + \infty]\\
u(0,x)=f_{ini}(x)
\end{array}\right.
\end{displaymath}](img42.png)
![\includegraphics[width=5in]{IMAGES/lignesCaracteristiques.eps}](img45.png)
![]() et
et ![]() ailleur, on va observer son déplacement le long des caractéristiques)
ailleur, on va observer son déplacement le long des caractéristiques)