L'étude de la stabilité de ce schéma va nous servir d'exemple pour présenter deux notions importantes, la
dissipation artificielle (liée au comportement en amplitude de l'erreur) et la dispersion (liée au comportement
en phase de l'erreur).
Avant toute chose, il est nécessaire de remarquer que l'erreur numérique et la solution exacte ont les
mêmes propriétés de croissance dans le temps. Les erreurs dans un système stable ne croissent donc pas dans
le temps.
La méthode de stabilité est celle de von Neumann (ou de Fourier).
L'erreur initiale (à ![]() ) y est décrite sous la forme d'une série de Fourier :
) y est décrite sous la forme d'une série de Fourier :
![\begin{displaymath}
\epsilon(x,0)= \sum_m \epsilon_m (x,0) = \sum_m \epsilon_{0_m} \exp{[i \frac{2 \pi x_j}{\lambda_m}]}
\end{displaymath}](img272.png)
avec ![]() une longueur d'onde et
une longueur d'onde et
![]() le nombre d'onde correspondant. Le
maillage implique :
le nombre d'onde correspondant. Le
maillage implique :
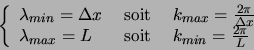
![]() et
et ![]() représentent le min. et le max. de la gamme finie de longueurs d'ondes. Cette
gamme contient
représentent le min. et le max. de la gamme finie de longueurs d'ondes. Cette
gamme contient
![]() points de discrétisation.
points de discrétisation.
On suppose que l'erreur pour chaque mode de Fourier est sous la forme :
de sorte que
![]() .
Il faut bien noter ici le terme
.
Il faut bien noter ici le terme ![]() puissance
puissance ![]() (
(![]() l'itération). L'équation de l'erreur est :
l'itération). L'équation de l'erreur est :
En développant (avec
![]() ), on obtient :
), on obtient :
Or, on a :
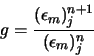
![]() est le facteur d'amplification pour le mode de Fourier
est le facteur d'amplification pour le mode de Fourier ![]() . La condition de stabilité est donc :
. La condition de stabilité est donc :
où
![]() est le nombre de courant.
est le nombre de courant.
Une condition équivalente de stabilité est
![]() (poser
(poser
![]() ).
).
Le facteur d'amplification peut aussi se poser sous la forme :
![\begin{displaymath}
g = \vert g\vert e^{i \varphi} =
\underbrace{\sqrt{\cos{(k_...
...\tan^{-1}[- \nu \tan{(k_m \Delta x)}]}}_{\textrm{d\'ephasage}}
\end{displaymath}](img291.png)
Le déphasage s'interprète comme la translation de chaque mode de Fourier dans le schéma.
![\includegraphics[width=5in]{IMAGES/dispersion1.eps}](img292.png)
![\includegraphics[width=5in]{IMAGES/dispersion2.eps}](img293.png)
Si ![]() et
et ![]() (pour chaque mode de Fourier) on n'a pas d'erreur d'amplitude ni de phase.
On observe donc ni dissipation artificielle (erreur d'amplitude) ni dispersion (erreur de phase).
(pour chaque mode de Fourier) on n'a pas d'erreur d'amplitude ni de phase.
On observe donc ni dissipation artificielle (erreur d'amplitude) ni dispersion (erreur de phase).