Étude de la diffusion numérique

En général les équations hyperboliques ont peu ou pas de dissipation. Toutefois, le schéma numérique induit souvent de la dissipation artificielle (perte d'amplitude). Il se peut aussi que la vitesse de propagation de l'onde soit changée par dispersion artificielle.

En effectuant des décompositions de Taylor pour $u_{j}^{n+1}$ et pour $u_{j-1}^{n}$ (pas besoin de toucher à $u_n^j$) et en les injectant dans le schéma, on obtient :

$$\underbrace{u_t + c u_x}_{\textrm{eq. d'onde}} = \underbrac... ..._{ttt} - \frac{\Delta x^2}{6} u_{xxx}+ \cdots}_{\textrm{E.T.}}$$

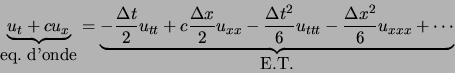
En éliminant toutes les dérivées temporelles à droite, on obtient :

$$\begin{array}{lcl} u_t + c u_x & = & - \frac{c^2 \Delta t}{2... ...ht] u_{xx} + c \Delta x^2 (\cdots) u_{xxx} + \cdots \end{array}$$

Cette dernière équation est l'équation modifiée. Le terme de droite est une autre écriture de l'erreur de troncature. On peut remarquer que l'E.T. contient un terme en $(.) u_{xx}$. Celui-ci est similaire à un terme visqueux dans l'équation de Navier Stokes. Quand $\frac{c \Delta t}{\Delta x} \neq 1$, on introduit donc de la viscosité artificielle dans la solution.

Si le terme principal de l'E.T. est du type $(.) u_{xxx}$, on observe à la place un phénomène de dispersion qui change les relations de phase entre les différentes ondes.

D'un point de vue général si le terme dominant dans l'E.T. contient une dérivée :

• paire : On observe principalement des erreurs de dissipation. C'est typiquement le cas pour les scémas d'ordre un.
• impaire : on observe principalement des erreurs de dispersion (ou wiggles). C'est généralement le cas pour les schémas d'ordre deux.
  

L'effet combiné de la dispersion et de la dissipation est la diffusion numérique. Il est important d'être conscient qu'il existe une relation entre le facteur d'amplification $g$ de l'analyse de Von Neumann et l'équation modifiée.