Adaptation des schémas $1D$

Les techniques utilisées précédement posent des difficultés. Voyons deux exemples significatifs :

1. Simple schéma explicite :
   
   $$\frac{u_{i,j}^{n+1}-u_{i,j}^{n}}{\Delta t} = \alpha \left[ \... ...{u_{i,j+1}^{n}-2u_{i,j}^{n}+u_{i,j-1}^{n}}{\Delta y^2} \right]$$
   
   

   Pour résoudre l'évolution du système, on pose le schéma sous la forme :
   

   $$u_{i,j}^{n+1} = A u_{i,j}^{n} + B u_{i+1,j}^{n} + C u_{i-1,j}^{n} + D u_{i,j+1}^{n} + E u_{i,j-1}^{n}$$
   
   

   avec :
   

   $$\left\{ \begin{array}{l} A = 1- 2 \alpha \frac{\Delta t}{\De... ...}{\Delta y^2}\\ i \in [1,I]\\ j \in [1,J] \end{array}\right.$$
   
   

   On considère $i=\{1, 2, ..., I\}$ et $j=\{1, 2, ..., J\}$. Les conditions limites sont alors les $u_{0,j} , u_{I+1,j},u_{i,0} , u_{i,J+1}$ que l'on considère comme des constantes (conditions limites de Dirichlet).
   

   On constate que $B=C$ et $D=E$. Nous les différencions pour une meilleure compréhension de la méthode. On pose :
   

   $$U^n = \left( \begin{array}{c} u_{1,1}\\ u_{1,2}\\ \vdots\\... ..._{I-1,J}\\ u_{I,1}\\ \vdots\\ u_{I,J}\\ \end{array}\right)$$
   
   

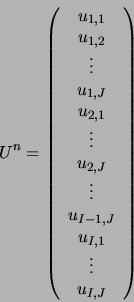
   La forme matricielle du problème est alors :
   

   $$U^{n+1}= M U^n + V$$
   
   

   M est une matrice $(I*J , I*J)$. Elle a la forme d'une matrice par blocs :
   

   $$M= \left( \begin{array}{ccccc} \begin{array}{\vert c\vert} \... ...c\vert} \hline M_c \\ \hline \end{array}\\ \end{array}\right)$$
   
   

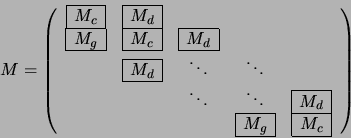
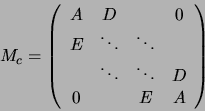
   Chaque bloc est de taille $(J*J)$ et :
   

   $$\begin{array}{lcr} M_g = \left( \begin{array}{ccc} C&&0\\ &... ...ccc} B&&0\\ &\ddots&\\ 0&&B\\ \end{array}\right) \end{array}$$
   
   

   
   

   $$M_c = \left( \begin{array}{cccc} A&D&&0\\ E&\ddots&\ddots&\\ &\ddots&\ddots&D\\ 0&&E&A\\ \end{array}\right)$$
   
   

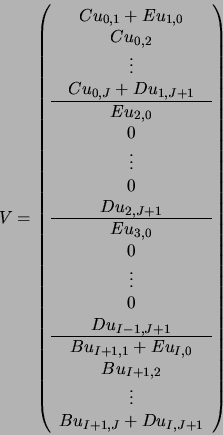
   Comme dans le cas $1D$, le vecteur $V$ de taille $(I*J)$ contient les conditions aux limites :
   

   $$V= \left( \begin{array}{c} C u_{0,1}+ E u_{1,0}\\ C u_{0,2}... ...1,2}\\ \vdots\\ B u_{I+1,J} + D u_{I,J+1} \end{array}\right)$$
   
   

   Remarque : Pour résoudre ce genre de problèmes sous Matlab, il est intéressant de déclarer $M$ comme une matrice creuse (sparse matrix). Dans un langage tel que le C ou Fortran on codera la matrice de façon intelligente. On ne rentrera que les bandes non nulles de la matrice et adaptera la multiplication multiplication matricielle au type de codage choisi.
   

   La condition de stabilité de ce schéma est :
   

   $$\alpha \Delta t \left[ \frac{1}{\Delta x^2} +\frac{1}{\Delta y^2} \right] \leqslant \frac{1}{2}$$
   
   

   En prenant $\Delta x = \Delta y$, la condition de stabilité est :
   

   $$\frac{\alpha \Delta t}{ \Delta x^2} \leqslant \frac{1}{2}$$
   
   

   Cette condition est encore plus restrictive que dans le cas $1D$!

2. Schéma de Crank-Nicolson :
   
   $$\frac{u_{i,j}^{n+1}-u_{i,j}^{n}}{\Delta t} = \frac{\alpha}{2} (\delta_x^2 + \delta_y^2)(u_{i,j}^{n+1} + u_{i,j}^{n})$$
   
   

   avec les notations :
   

   $$\begin{array}{l} \delta_x^2 u_{i,j}^n = \frac{u_{i+1,j}^{n} ... ...1}^{n} - 2 u_{i,j}^{n} + u_{i,j-1}^{n}}{\Delta y^2} \end{array}$$
   
   

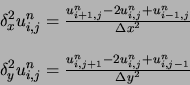
   Ce schéma est inconditionnellement stable même en $2D$. On a cependant perdu la structure tridiagonale du système $1D$. Le système est de type :
   

   $$a u_{i,j-1}^{n+1} + b u_{i-1,j}^{n+1} + c u_{i,j}^{n+1} + b u_{i+1,j}^{n+1} + a u_{i,j+1}^{n+1} = d_{i,j}^n$$
   
   

   avec :
   

   $$\left\{ \begin{array}{l} a = - \frac{\alpha}{2} \frac{\Delta... ...a t}{2} (\delta_x^2 + \delta_y^2) u_{i,j}^n \end{array}\right.$$
   
   

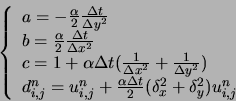
   Pour résoudre le système, il est alors nécessaire d'inverser (schéma implicite oblige) une matrice de taille $(I*J , I*J)$. Il faut alors absolument utiliser un algorithme d'inversion adapté (ici Gauss-Seidel par exemple).