Méthode ADI

ADI signifie Alternating Direction Implicit (Peaceman, Rachford et Douglas 1955). Cette méthode rentre dans la catégorie des méthode du pas fractionnaire ou méthode de splitting. C'est un schéma implicite à deux pas. Il est de type prédiction-correction :

$$\begin{array}{lll} \textrm{Pas 1 : }& \frac{u_{i,j}^{n+1/2} ... ...^2 u_{i,j}^{n+1}] \qquad & \textrm{(correction)}\\ \end{array}$$

avec les mêmes notations que précédement :

$$\begin{array}{l} \delta_x^2 u_{i,j}^n = \frac{u_{i+1,j}^{n} ... ...1}^{n} - 2 u_{i,j}^{n} + u_{i,j-1}^{n}}{\Delta y^2} \end{array}$$

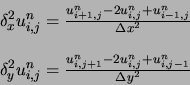
On avance d'une moitié de pas à chaque fois. A chaque demi pas, les terme implicites ($n+1/2$ au pas 1 et $n+1$ au pas 2) ne portent que sur une des deux dimensions (ici $x$ au pas 1 et $y$ au pas 2). Nous avons vu dans l'exemple précédent (schéma de Cranck Nicolson 2D) que résoudre le problème de manière implicite sur $\vec{e_x}$ et $\vec{e_y}$ à la fois demande l'inversion d'une matrice diagonale par blocs. Avec la méthode ADI, on inverse deux fois une matrice tridiagonale ce qui est algorithmiquement préférable. On utilisera ici l'algorithme de Thomas par exemple.

La méthode ADI a une erreur de troncature d'ordre $\bigcirc (\Delta t^2, \Delta x^2, \Delta y^2)$ et est inconditionnellement stable.

Il existe évidement d'autres méthodes comme la méthode ADE, la méthode Keller Box... En général, les méthodes implicites sont recommandées car leur stabilité est meilleure.