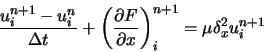
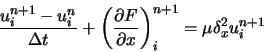
avec :
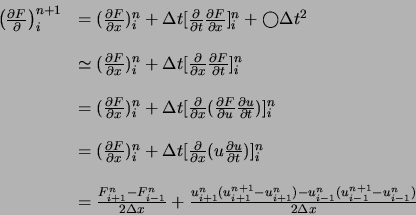
Ici, l'erreur de troncature est d'ordre
![]() pour le schéma complet. Nous obtenons donc un système
linéaire d'équations algébriques pour le temps
pour le schéma complet. Nous obtenons donc un système
linéaire d'équations algébriques pour le temps ![]() ce qui donne un système tridiagonal. Ce schéma est inconditionnellement
stable. La précision temporelle peut être améliorée par le schéma suivant (inconditionnellement stable et d'E.T. d'ordre
ce qui donne un système tridiagonal. Ce schéma est inconditionnellement
stable. La précision temporelle peut être améliorée par le schéma suivant (inconditionnellement stable et d'E.T. d'ordre
![]() ) :
) :
![\begin{displaymath}
\begin{array}{l}
\frac{u_{i}^{n+1}-u_{i}^{n}}{ \Delta t} + \...
...}{2} \mu [\delta_x^2 u_i^n + \delta_x^2 u_i^{n+1} ]
\end{array}\end{displaymath}](img415.png)
Remarque : si le schéma de Bridley- Mc Donald est utilisé directement pour l'équation de Burgers ![]() , on n'obtient pas un
système d'équations algébriques tridiagonal. Une solution est d'utiliser la procédure ADI à deux pas.
, on n'obtient pas un
système d'équations algébriques tridiagonal. Une solution est d'utiliser la procédure ADI à deux pas.