Méthode de la compressibilité artificielle

Cette méthode est dédiée à la résolution des équations de N.S. stationnaires :

$$\left\{ \begin{array}{l} (\vec{u}.\vec{\nabla}) \vec{u} + \v... ...bla^2 \vec{u}\\ \vec{\nabla} . \vec{u} = 0 \end{array}\right.$$

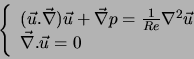
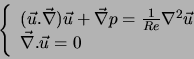
Elle se caractérise par :

1. Introduction d'un temps fictif $\tau$. On a $\vec{u}$ et $p$ qui dépendent de $\tau$.
2. On se ramène au problème compressible (la solution stationnaire reste incompressible!) :
   
   $$\left\{ \begin{array}{l} \frac{\partial p}{\partial \tau} + ... ...c{\nabla} p = \frac{1}{Re} \nabla^2 \vec{u} \end{array}\right.$$
   
   

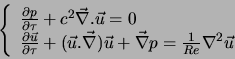
   Les équations sont du type hyperbolique-parabolique. Ici, la transitoire n'est pas physique mais (on l'espère) l'état stationnaire est bon !
   

   Le paramètre $c^2$ est arbitraire. Il est choisi de manière optimale pour assurer une convergence rapide. Il s'agit en effet d'une vitesse du son artificielle

La résolution peut s'effectuer avec une méthode numérique adaptée : La méthode MAC.