Méthode Marker And Cell (MAC)

Cette méthode tire ses origines dans Harlow & Welch 1965 et Welch & al 1966. Elle utilise un maillage décallé. La pression, la vitesse suivant $X$ et la vitesse suivant $Y$ ne sont pas calculées aux mêmes points.

L'équation sous forme discrète, pour une discrétisation de type Jacobi (explicite) peut s'écrire sous la forme :

• Vitesse suivant $X$ :
  
  $$\begin{array}{l} \frac{u_{i+1/2,j}^{n+1}-u_{i+1/2,j}^{n}}{\D... ...n}-2u_{i+1/2,j}^{n}+u_{i+1/2,j-1}^{n}}{\Delta y^2}] \end{array}$$
  
  

• Vitesse suivant $Y$ :
  
  $$\begin{array}{l} \frac{v_{i,j+1/2}^{n+1}-v_{i,j+1/2}^{n}}{\D... ...n}-2v_{i,j+1/2}^{n}+v_{i-1,j+1/2}^{n}}{\Delta x^2}] \end{array}$$
  
  

• Masse :
  
  $$\frac{p_{i,j}^{n+1}-p_{i,j}^{n}}{\Delta \tau} + c^2 \left[ \... ... + \frac{v_{i,j+1/2}^{n}-v_{i,j-1/2}^{n}}{\Delta y} \right] =0$$
  
  

Un schéma de Gauss-Seidel converge plus rapidement. Son écriture est la même que Jacobi en remplacant les $n$ par des $n+1$ dans les termes en espace.

Au niveau de la frontière du domaine, on a un problème. Des points nécéssaires pour le calcul sont à l'exterieur du domaine physique (classique).

Ici, on résoud le problème de cette sorte :

• On ne prend pas en compte les points de pression sur la frontière. Les conditions de pression n'y sont pas nécessaires.
• Pour respecter la condition d'adhérence pour la vitesse, on procède avec (en supposant que les parois sont fixes) :
  
  $$\left\{ \begin{array}{l} v_{i,j+1/2} = 0\\ u_{i+1/2,j+1} = - u_{i+1/2,j} \end{array}\right.$$
  
  

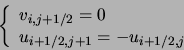
  La deuxième ligne exprime une technique de réflexion. Elle exprime le fait que la vitesse est nulle sur la paroi (ici en $u_{i+1/2,j+1/2}$) :

  

  Frontière du domaine physique

  En effet dans le schéma on aura :
  

  $$u_{i+1/2,j+1/2} \approx \frac{u_{i+1/2,j}+u_{i+1/2,j+1}}{2} = 0$$
  
  

On peut aussi résoudre le problème en utilisant un autre maillage : on met la pression au centre de la cellule, et on fait coïncider la grille avec le domaine (et sa frontière) :

En général, l'avantage de la grille décalée est qu'il n'y a pas de couplage entre vitesse et pression. De plus, on n'a pas besoin d'une condition de pression sur la frontière. En effet, pour une frontière solide, cette condition s'écrit :

$$\vec{n}. \vec{\nabla} p = \vec{n} . \frac{1}{Re} \nabla^2 \v... ...rtial p}{\partial n} = \frac{1}{Re} \nabla^2 \vec{u} . \vec{n}$$

Cette C.L. pour $p$ est satisfaite de manière implicite par le schéma MAC (l'approximation d'une couche limite est : $\frac{\partial p}{\partial y}=0$). On peut noter que si on prend la composante tangentielle des équations de Navier-Stokes à la frontière, $\vec{\tau}.\vec{\nabla}p = \vec{\tau} . \frac{1}{Re} \nabla^2 \vec{u}$ soit $\frac{\partial p}{\partial \tau} = \frac{1}{Re} \nabla^2 (\vec{u}.\vec{\tau})$, on a une autre C.L. pour $p$ :

$$\left\{ \begin{array}{l} \textrm{Composante normale : } \fra... ...artial p}{\partial x} = \frac{1}{Re} u_{yy} \end{array}\right.$$

On a donc redondance des conditions limites.