On ne peut pas analyser la stabilité d'un schéma pour une équation non linéaire, il est nécessaire d'en faire une approximation.
On linéarise l'équation sous forme non-conservative (
![]() ) avec
) avec ![]() et
et ![]() des constantes, on élimine le décalage des cellules et on oublie la pression :
des constantes, on élimine le décalage des cellules et on oublie la pression :
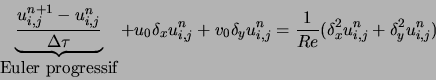
Tout comme dans le chapitre ![]() ,
, ![]() représente les différences centrées.
On suppose l'erreur de la forme :
représente les différences centrées.
On suppose l'erreur de la forme :
alors :

et :
Finalement, avec l'hypothèse
![]() et en prenant
et en prenant
![]() et
et
![]() , on a :
, on a :
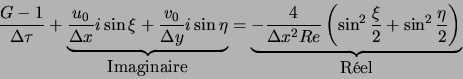
donc :

Il y a évidement une limite sur la longueur d'onde que l'on peut capturer numériquement avec
un maillage donné ; il faut au moins deux intervales ![]() pour capturer une onde (th. de Shannon).
pour capturer une onde (th. de Shannon).
Soit ![]() le nombre d'onde, on a alors comme longueur d'onde
le nombre d'onde, on a alors comme longueur d'onde
![]() et :
et :
avec ![]() la longueur du domaine selon
la longueur du domaine selon ![]() . Ainsi :
. Ainsi :
On choisi donc la valeur maximale de ![]() et
et ![]() comme :
comme :
dans ce cas :
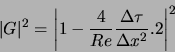
Le schéma est alors stable si :
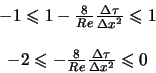
soit :
Si on avait choisi pour ![]() et
et ![]() :
:
on aurait eu :
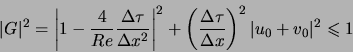
pour la stabilité, soit :
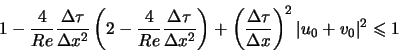
En majorant le terme à gauche et en simplifiant, on a :
donc :
Cette condition donne la limite de stabilité convective.
Les deux limites trouvées doivent être satisfaites. Une troisième analyse de stabilité peut être effectuée en éliminant
le terme non-linéaire et en cherchant à calculer la stabilité de l'écoulement de Stokes. Dans ce cas, on peut trouver :

et on trouve une méthode sur ![]() .
.
Une petite remarque avant de terminer cette section. Dans la section suivante, on trouve la méthode fonction de courant, vorticité qui peut s'appliquer pour des écoulements stationnaires avec une méthode similaire à celle de la compressiblité artificielle.