



suivant: Méthode de projection implicite
monter: Écoulement instationnaire
précédent: Écoulement instationnaire
Table des matières
Pour la résolution des équations de Navier Stokes instationnaires, une méthode explicite au pas fractionnaire
et d'ordre 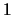 en temps est la méthode de projection :
en temps est la méthode de projection :
- Pas 1 : On pose N.S. sans pression :
- Pas 2 : On obtient la pression par l'équation :
Cette équation produit un champ de vitesse à divergence nulle :
- Pas 3 : On calcule :
En éliminant 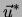 dans le pas
dans le pas 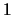 et le pas
et le pas 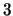 , on retrouve bien :
, on retrouve bien :
Les C.L. pour la pression doivent satisfaire une relation de compatibilité. Soit 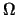 le domaine et
le domaine et 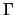 la frontière, alors le
deuxième pas implique :
la frontière, alors le
deuxième pas implique :
Cette relation est la relation de compatibilité.
On obtient aussi, depuis le pas 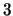 :
:
donc :
C'est une condition de Neumann de pression. Par intégration sur 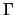 , on obtient :
, on obtient :
En pratique :
- Pas 1 :
On calcule
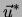 aux points intérieurs mais pas à la frontière (
aux points intérieurs mais pas à la frontière (
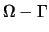 ). On impose
). On impose
 quelconque
sur la frontière. Un bon choix est
quelconque
sur la frontière. Un bon choix est
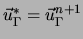
- Pas 2 :
On calcule
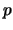 sur
sur 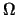 et impose
et impose
 . C'est l'approximation d'une couche limite sur
une paroi solide. Si la frontière n'est pas une paroi, il faut itérer entre le pas
. C'est l'approximation d'une couche limite sur
une paroi solide. Si la frontière n'est pas une paroi, il faut itérer entre le pas  et le pas
et le pas 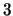 .
.
- Pas 3 :
On calcule alors
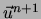 sur
sur 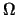 avec
avec
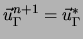 pour garder
pour garder
 et
et
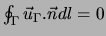 .
.
La méthode explicite impose des limitations sévères sur le pas de temps, aussi bien du point de vue visqueux que du
non visqueux. Il est donc recommandé d'utiliser des schémas implicites.




suivant: Méthode de projection implicite
monter: Écoulement instationnaire
précédent: Écoulement instationnaire
Table des matières
RISSER Laurent
2006-02-04
![]() en temps est la méthode de projection :
en temps est la méthode de projection :
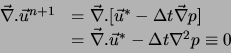
![]() dans le pas
dans le pas ![]() et le pas
et le pas ![]() , on retrouve bien :
, on retrouve bien :
![]() le domaine et
le domaine et ![]() la frontière, alors le
deuxième pas implique :
la frontière, alors le
deuxième pas implique :

![]() :
:
![]() , on obtient :
, on obtient :
