Cette procédure est basée sur une série d'opérations d'estimation - correction. La vitesse est tout d'abord calculée à partir de
l'équation de continuité en faisant une estimation sur le champ de pression. La pression et la vitesse sont ensuite corrigés pour
satisfaire la continuité. On répète ce processus jusqu'à la convergence. La différence entre cette méthode et le méthode MAC
ou bien les méthode de projection est la manière dont on corrige la pression et la vitesse.
Dans cette procédure, on pose la pression réelle ![]() telle que :
telle que :
avec ![]() la valeur estimée de la pression et
la valeur estimée de la pression et ![]() la correction sur la pression. De la même manière, la vitesse réelle s'écrit :
la correction sur la pression. De la même manière, la vitesse réelle s'écrit :

On relie les corrections sur la pression et la vitesse à partir d'une approximation de l'équation de mouvement :
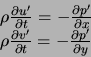
En considérant la correction de pression comme nulle à l'itération précédante et
![]() , on a :
, on a :
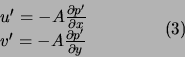
avec
![]() .
.
En combinant les équations ![]() et
et ![]() , on obtient :
, on obtient :
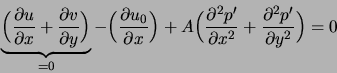
soit :
où ![]() est le vecteur d'estimation de la vitesse. On a alors une équation de Poisson à résoudre. On pourra utiliser l'algorithme
de Gauss-Seidel pour la résoudre. On peut aussi résoudre l'équation par une évolution de l'algorithme (Raithly & Schneider 1979) :
est le vecteur d'estimation de la vitesse. On a alors une équation de Poisson à résoudre. On pourra utiliser l'algorithme
de Gauss-Seidel pour la résoudre. On peut aussi résoudre l'équation par une évolution de l'algorithme (Raithly & Schneider 1979) :
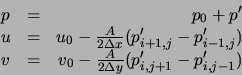
On pourra remarquer que ![]() tend à être surestimé. On utilise alors souvent
tend à être surestimé. On utilise alors souvent
![]() à la place de
à la place de ![]() où
où ![]() est un coefficient de sous relaxation.
est un coefficient de sous relaxation.