En dimension deux, il est avantageux d'utiliser une formulation fonction de courant - vorticité. Dans cette approche,
on applique un changement de variables qui remplace les composantes de vitesse par la vorticité ![]() et la fonction
de courant
et la fonction
de courant ![]() . On n'a donc pas a un schéma en variables primitives comme précédement.
Soit
. On n'a donc pas a un schéma en variables primitives comme précédement.
Soit
![]() la vitesse ; l'équation de transport visqueux est alors :
la vitesse ; l'équation de transport visqueux est alors :
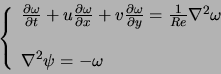
avec :
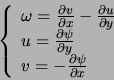
L'équation en première ligne est parabolique et celle en deuxième ligne est elliptique. On peut noter que le terme
![]() a disparu car
a disparu car
![]() est dans le plan
est dans le plan ![]() et
et ![]() est selon
est selon ![]() .
.
A chaque pas de ![]() , il faut résoudre une équation de Poisson, ce qui est coûteux. Si on cherche seulement l'état stationnaire,
on peut utiliser une méthode similaire à celle de la compressibilité artificielle. C'est la méthode pseudo-stationnaire :
, il faut résoudre une équation de Poisson, ce qui est coûteux. Si on cherche seulement l'état stationnaire,
on peut utiliser une méthode similaire à celle de la compressibilité artificielle. C'est la méthode pseudo-stationnaire :