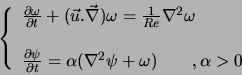
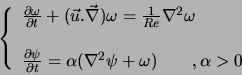
Les deux équations sont paraboliques. ![]() est un paramètre de relaxation nécessaire pour la convergence du schéma. La
variable
est un paramètre de relaxation nécessaire pour la convergence du schéma. La
variable ![]() représente, ici, un temps fictif. Pour la résolution,
on peut choisir pour une méthode implicite (ADI par exemple) ou explicite.
représente, ici, un temps fictif. Pour la résolution,
on peut choisir pour une méthode implicite (ADI par exemple) ou explicite.
Pour les conditions limites, on nomme ![]() le domaine et
le domaine et ![]() la frontière sur laquelle
la frontière sur laquelle ![]() est connu (
est connu (
![]() ).
).
![\includegraphics[width=4in]{IMAGES/CLfonctionCourant.eps}](img539.png)
Dans le cas des conditions limites, on interprète
![]() et
et
![]() par :
par :
On a :
On néglige la constante. Soit la fonction ![]() telle que :
telle que :
Ici, ![]() et
et ![]() correspondent à un noeud de l'espace discrétisé (l'intégrale est sur une partie de la frontière). Alors, sur
correspondent à un noeud de l'espace discrétisé (l'intégrale est sur une partie de la frontière). Alors, sur ![]() :
:
Avec
![]() . On a donc une condition de Dirichlet et une de Neumann.
Evidemment, il faudra imposer seulement une de ces deux conditions.
. On a donc une condition de Dirichlet et une de Neumann.
Evidemment, il faudra imposer seulement une de ces deux conditions.
![\includegraphics[width=4in]{IMAGES/CLvorticite.eps}](img547.png)
On a :
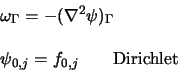
On cherche :
Pour calculer ![]() , il nous faut connaitre
, il nous faut connaitre ![]() et
et ![]() . On trouve
. On trouve ![]() facilement :
facilement :
Pour ![]() , on utilise un développement de Taylor :
, on utilise un développement de Taylor :

donc :
et ainsi :
![\begin{displaymath}
\omega_{0,j} = - \left[ \frac{2}{\Delta x^2} (\psi_{1,j} - \...
...ace{\psi_{0,j}}_{f_{0,j}} - \Delta x g_{0,j}) + f_{yy} \right]
\end{displaymath}](img557.png)
Il est aussi possible d'approximer ![]() par une autre méthode. On commence par écrire :
par une autre méthode. On commence par écrire :
Cette égalité est seulement satisfaite à la convergence du schéma car avant, ![]() n'a pas la bonne valeur.
On peut alors écrire comme C.L. sur
n'a pas la bonne valeur.
On peut alors écrire comme C.L. sur ![]() à chaque pas de
à chaque pas de ![]() (algorithme de descente avec
(algorithme de descente avec ![]() comme paramètre de
relaxation) :
comme paramètre de
relaxation) :
![\begin{displaymath}
\omega_{0,j}^{n+1} = \omega_{0,j}^{n} - \gamma \left[ \frac{\psi_{1,j}^{n} - f_{0,j}}{\Delta x} -g_{0,j} \right]
\end{displaymath}](img561.png)
A la convergence, on a :
et ![]() a la bonne valeur, et donc on a bien (correcte à l'ordre
a la bonne valeur, et donc on a bien (correcte à l'ordre ![]() ) :
) :