On considère la fonction ![]() de
de ![]() dans
dans ![]() aux points équirépartis
aux points équirépartis
![]() avec
avec ![]() . On suppose
. On suppose ![]() périodique sur un intervalle de longueur
périodique sur un intervalle de longueur
![]() . On a :
. On a :
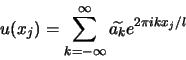
avec
![]() les points dits de collocation. On peut visualiser les
les points dits de collocation. On peut visualiser les
![]() comme le poids
qu'a la fréquence
comme le poids
qu'a la fréquence ![]() dans la fonction
dans la fonction ![]() . Les
. Les
![]() se calculent par la formule suivante :
se calculent par la formule suivante :
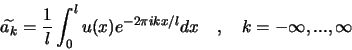
En pratique, on ne peut pas calculer le poids d'une infinité de fréquences dans un signal discrétisé comme
c'est le cas avec les ![]() . On ne pourra obtenir les
. On ne pourra obtenir les
![]() que pour
que pour
![]() sachant que
sachant que
![]() (avec
(avec
![]() le conjugué de
le conjugué de
![]() )
si
)
si ![]() est dans
est dans ![]() . On considère alors
. On considère alors
![]() , l'approximation pseudo-spectrale de
, l'approximation pseudo-spectrale de ![]() :
:
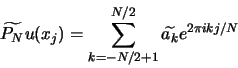
où les termes
![]() sont calculés par la formule suivante (on utilise la notation
sont calculés par la formule suivante (on utilise la notation ![]() ) :
) :
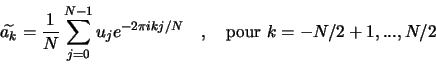
On parle d'approximation pseudo-spectrale et non spectrale quand ![]() est fini. En effet, on considère comme
négligeable le poids de toutes les fréquences que l'on aurait considérées en poussant
est fini. En effet, on considère comme
négligeable le poids de toutes les fréquences que l'on aurait considérées en poussant ![]() vers l'infini.
vers l'infini.
On peut alors calculer facilement l'approximation des dérivées
![]() de
de ![]() :
:

Il requière ![]() calculs pour obtenir tous les
calculs pour obtenir tous les
![]() . Cet impact peut
être largement réduit (
. Cet impact peut
être largement réduit (
![]() calculs) si l'on utilise l'agorithme de Transformée de Fourier Rapide.
En comparaison, les approximations aux différences finies demandent
calculs) si l'on utilise l'agorithme de Transformée de Fourier Rapide.
En comparaison, les approximations aux différences finies demandent ![]() calculs. On peut alors se demander
quel est l'intérêt de l'approximation pseudo-spectrale. Il réside dans la qualité d'approximation des dérivées spatiales.
Quand une méthode de différences finies classique créé une erreur d'approximation de la dérivée
de l'ordre d'une puissance (faible) de
calculs. On peut alors se demander
quel est l'intérêt de l'approximation pseudo-spectrale. Il réside dans la qualité d'approximation des dérivées spatiales.
Quand une méthode de différences finies classique créé une erreur d'approximation de la dérivée
de l'ordre d'une puissance (faible) de ![]() , le terme d'erreur sur une dérivée décroît exponentiellement avec
, le terme d'erreur sur une dérivée décroît exponentiellement avec ![]() avec une approximation pseudo-spectrale. La qualité de la dérivation est incomparablement meilleure. On parle de méthode
d'ordre supérieur.
avec une approximation pseudo-spectrale. La qualité de la dérivation est incomparablement meilleure. On parle de méthode
d'ordre supérieur.