



suivant: Méthodes pseudo-spectrales pour la
monter: Méthodes spectrales
précédent: Approximation pseudo-spectrale
Table des matières
On calcule les
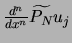 en les considérant comme le résultat de produits linéaires
avec les valeurs de
en les considérant comme le résultat de produits linéaires
avec les valeurs de 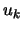 . Soit :
. Soit :
où  est l'approximation pseudo-spectrale de
est l'approximation pseudo-spectrale de
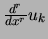 . On souhaite écrire l'opérateur
différentiel
. On souhaite écrire l'opérateur
différentiel 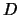 tel que
tel que
 . L'opérateur
. L'opérateur 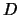 est nommé matrice de différentiation
pseudo-spectrale. On le construit en trois étapes :
est nommé matrice de différentiation
pseudo-spectrale. On le construit en trois étapes :
- A partir des
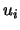
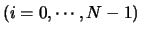 , on calcule les
, on calcule les
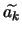
 en utilisant la transformée de Fourier.
En prenant soin de convertir les indexes, cette opération est strictement équivalente à une multiplication matricielle
en utilisant la transformée de Fourier.
En prenant soin de convertir les indexes, cette opération est strictement équivalente à une multiplication matricielle 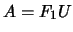 .
Le nombre d'opérations est alors en
.
Le nombre d'opérations est alors en  .
.
- Calcul des termes spectraux des dérivées
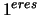 en multipliant chaque
en multipliant chaque 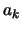 par
par 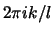 . Cette opération
est équivalente à un produit scalaire
. Cette opération
est équivalente à un produit scalaire 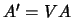 avec
avec
![$V=[2 \pi i (-N/2+1) / l, \cdots,2 \pi i (N/2) / l]$](img605.png) .
Le nombre d'opérations est ici en
.
Le nombre d'opérations est ici en 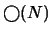 .
.
- A partir du résultat obtenu à l'étape précédente, on calcule les
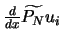 en utilisant une
transformée de Fourier inverse. Comme à la première étape, cette opération est strictement équivalente à une
multiplication matricielle par une matrice
en utilisant une
transformée de Fourier inverse. Comme à la première étape, cette opération est strictement équivalente à une
multiplication matricielle par une matrice
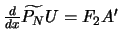 .
Le nombre d'opérations est encore en
.
Le nombre d'opérations est encore en  .
.
L'opérateur 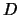 vaut alors :
vaut alors :
avec  la matrice dont la diagonale est égale à
la matrice dont la diagonale est égale à  et les autres termes sont nuls.
et les autres termes sont nuls.
L'opération est au final de complexité algorithmique 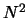 ce qui est rédhibitoire pour de grandes valeurs de
ce qui est rédhibitoire pour de grandes valeurs de 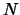 . Comme
cela a été évoqué dans la section précédente, en pratique, on réduit considérablement la complexité algorithmique
de l'opération en utilisant la Transformée de Fourier Rapide (en Anglais Fast Fourier Transform ou FFT). Pour cela,
. Comme
cela a été évoqué dans la section précédente, en pratique, on réduit considérablement la complexité algorithmique
de l'opération en utilisant la Transformée de Fourier Rapide (en Anglais Fast Fourier Transform ou FFT). Pour cela, 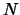 doit être une puissance de
doit être une puissance de  . Une transformée de Fourier passe d'une complexité
. Une transformée de Fourier passe d'une complexité 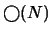 à une complexitée
à une complexitée
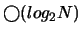 . La procédure de calcul de
. La procédure de calcul de
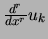 est alors la suivante :
est alors la suivante :
- A partir des
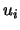
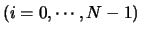 , on calcule les
, on calcule les
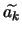
 en utilisant la FFT.
Le nombre d'opérations est maintenant en
en utilisant la FFT.
Le nombre d'opérations est maintenant en
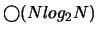 avec
avec 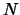 pour les
pour les 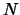
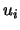 et
et 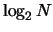 pour la FFT.
pour la FFT.
- Calcul des termes spectraux des dérivées
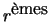 en multipliant chaque
en multipliant chaque 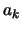 par
par
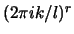 . L'opération
est toujours ici en
. L'opération
est toujours ici en 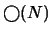 .
.
- A partir du résultat obtenu à l'étape précédente, calcule des
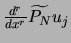 en utilisant une
FFT inverse. Comme à la première étape, le nombre d'opérations est en
en utilisant une
FFT inverse. Comme à la première étape, le nombre d'opérations est en
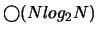 .
.
Au final, la complexité algorithmique est maintenant en
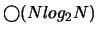 ce qui est beaucoup plus raisonnable. On ne
peut plus par contre considérer cette opération comme un produit matriciel mais plutôt comme une boîte noire, ce
qui n'est pas bien génant tant que les résultats sont les mêmes.
ce qui est beaucoup plus raisonnable. On ne
peut plus par contre considérer cette opération comme un produit matriciel mais plutôt comme une boîte noire, ce
qui n'est pas bien génant tant que les résultats sont les mêmes.




suivant: Méthodes pseudo-spectrales pour la
monter: Méthodes spectrales
précédent: Approximation pseudo-spectrale
Table des matières
RISSER Laurent
2006-02-04
![]() en les considérant comme le résultat de produits linéaires
avec les valeurs de
en les considérant comme le résultat de produits linéaires
avec les valeurs de ![]() . Soit :
. Soit :
![\begin{displaymath}
U = U^{(0)} =
\left[
\begin{array}{c}
u_0\\
\vdots\\
u_{N-...
...{c}
u_0^{(r)}\\
\vdots\\
u_{N-1}^{(r)}\\
\end{array}\right]
\end{displaymath}](img593.png)
![]() est l'approximation pseudo-spectrale de
est l'approximation pseudo-spectrale de
![]() . On souhaite écrire l'opérateur
différentiel
. On souhaite écrire l'opérateur
différentiel ![]() tel que
tel que
![]() . L'opérateur
. L'opérateur ![]() est nommé matrice de différentiation
pseudo-spectrale. On le construit en trois étapes :
est nommé matrice de différentiation
pseudo-spectrale. On le construit en trois étapes :
![]() vaut alors :
vaut alors :
![]() la matrice dont la diagonale est égale à
la matrice dont la diagonale est égale à ![]() et les autres termes sont nuls.
et les autres termes sont nuls.
![]() ce qui est rédhibitoire pour de grandes valeurs de
ce qui est rédhibitoire pour de grandes valeurs de ![]() . Comme
cela a été évoqué dans la section précédente, en pratique, on réduit considérablement la complexité algorithmique
de l'opération en utilisant la Transformée de Fourier Rapide (en Anglais Fast Fourier Transform ou FFT). Pour cela,
. Comme
cela a été évoqué dans la section précédente, en pratique, on réduit considérablement la complexité algorithmique
de l'opération en utilisant la Transformée de Fourier Rapide (en Anglais Fast Fourier Transform ou FFT). Pour cela, ![]() doit être une puissance de
doit être une puissance de ![]() . Une transformée de Fourier passe d'une complexité
. Une transformée de Fourier passe d'une complexité ![]() à une complexitée
à une complexitée
![]() . La procédure de calcul de
. La procédure de calcul de
![]() est alors la suivante :
est alors la suivante :
![]() ce qui est beaucoup plus raisonnable. On ne
peut plus par contre considérer cette opération comme un produit matriciel mais plutôt comme une boîte noire, ce
qui n'est pas bien génant tant que les résultats sont les mêmes.
ce qui est beaucoup plus raisonnable. On ne
peut plus par contre considérer cette opération comme un produit matriciel mais plutôt comme une boîte noire, ce
qui n'est pas bien génant tant que les résultats sont les mêmes.