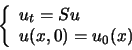
Ces méthodes sont aussi appelées méthodes de collocations.
On considère l'équation aux dérivées partielles de la forme :
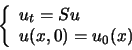
où ![]() est un opérateur différentiel spatial et
est un opérateur différentiel spatial et ![]() est considéré périodique. L'équation résolue est :
est considéré périodique. L'équation résolue est :
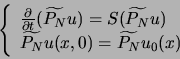
Par exemple considérons l'équation d'une onde suivante :
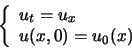
La manière la plus simple d'exprimer ce que l'on fait est d'utiliser l'opérateur différentiel ![]() vu à la précédente
section (même si en pratique on utilisera la FFT ce qui est strictement équivalent au niveau du résultat). L'opérateur
vu à la précédente
section (même si en pratique on utilisera la FFT ce qui est strictement équivalent au niveau du résultat). L'opérateur
![]() se présente sous la forme d'une matrice. Soit
se présente sous la forme d'une matrice. Soit
![]() , alors
l'équation est résolue en calculant :
, alors
l'équation est résolue en calculant :
où :
![\begin{displaymath}
\widetilde{U} =
\left[
\begin{array}{c}
\widetilde{u_0}\\
\vdots\\
\widetilde{u_{N-1}}
\end{array}\right]
\end{displaymath}](img620.png)
Pour le temps, on pourra par exemple utiliser la méthode d'Euler :
Pour résoudre n'importe quelle équation, on reproduit ce type de schéma. La résolution d'une équation non linéaire
pose cependant un problème technique dû au phénomène d'aliasing que nous développons dans la section suivante.