L'anti-aliasing

L'alisasing est dû à la périodicité de période $N$ des coefficients de Fourier :

$$\widetilde{a_{k+N}} = \frac{1}{N} \sum_{j=0}^{N-1} u_j e^{- ... ...{j=0}^{N-1} u(x_j) e^{- 2 \pi i (k) j /N} = \widetilde{a_k} .$$

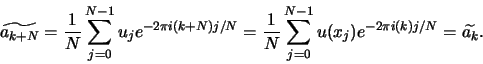
Cette périodicité créé une équivalence entre un terme de fréquence comprise dans le spectre que l'on a défini pour reconstruire notre signal et une fréquence à l'exterieur de ce spectre. Prendre en considération une fréquence trop haute dans la reconstruction se traduit donc par la création d'un artefact de reconstruction.

Considérons maintenant le terme non linéraire $v(x) w(x)$ d'une EDP que l'on souhaite résoudre par une méthode pseudo spectrale. Son approximation pseudo spectrale est :

$$\widetilde{P_N} v(x_j) w(x_j)= \sum_{k = -N/2+1}^{N/2} \wide... ...m_{k' = -N/2+1}^{N/2} \widetilde{w_{k'}} e^{ 2 \pi i k' j / N}$$

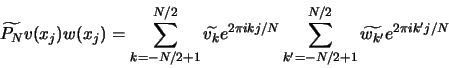
Ce qui est aussi égal à :

$$\widetilde{P_N} v(x_j) w(x_j)= \sum_{k = -N/2+1}^{N/2} \sum_... ... \widetilde{v_k} \widetilde{w_{k'}} e^{ 2 \pi i (k+k') j / N}$$

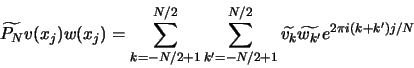
Tant que $-N/2+1 \leq k+k' \leq N/2$, on n'a pas de problème. Par contre dès que l'on sort de ce domaine, on reconstruit des fréquences qui n'ont pas été prévues dans notre spectre. On créé alors un artefact de reconstruction. Si le signal étudié à été hautement échantillonné à la vue des fréquences qu'il contient, l'artefact peut être considéré comme négligeable. Cependant, dans le cas général un traitement anti-aliasing s'impose.

Tout d'abord, observons pour le couple $(k,k')$, ( $[k,k'] \in [-N/2+1,\cdots, N/2]^2$) les valeurs qui posent problème :

Les couples $(k,k')$ créant un alias sont ceux pour lesquels $k+k'>N/2$ ou $k+k'<-N/2+1$. On pourrait pour traiter ces couples en utilisant la formule de transformation de Fourier via produit matriciel en ajoutant un test sur les $k+k'$. Cependant, comme nous l'avons vu plus tôt, il est nettement plus avantageux en terme de temps de calculs d'utiliser des FFT. Ces denières sont assimilées ici à des boîtes noires qu'on ne peut modifier. L'anti-aliasing doit alors s'effectuer ailleurs que dans la tranformation de Fourier.

Une solution largement utilisée est, une fois dans le domaine spectral, d'augmenter la taille de $\widetilde{v}$ et de $\widetilde{w}$ en rajoutant des $0$ sur les hautes fréquences créées. Formellement, on part du spectre de $\widetilde{v}$ et de $\widetilde{w}$ avec $k$ et $k'$ compris entre $-N/2+1$ et $N/2$ pour créer un spectre avec $k$ et $k'$ compris entre $-M/2+1$ et $M/2$ (avec $M>N$) en rajoutant des $0$ aux nouveaux indices.

Ceci revient mathématiquement à reconstruire le signal à partir des $\widetilde{v_k}$ et $\widetilde{w_{k'}}$ existants avec un maillage plus fin puis de le repasser dans le domaine fréquenciel. Comme on peut le voir sur l'illustration suivante, il suffit de prendre $M=3N/2$ pour éviter l'aliasing. En pratique on prendra le plus souvent $M=2N$ car, la FFT demande des signaux discrets de la taille d'une puissance de $2$. Le facteur $3/2$ sera toutefois utilisé dans certains cas car des versions dérivées de la FFT permettent d'effecuer une transformation de Fourier (ou de Fourier inverse) pour des signaux de dimension $2^m 3^n 5^p...$ ($m,n,p$ des entiers). Elles sont cependant plus lentes que la FFT originale. Il y a donc un compromis à faire entre ce qui est gagné avec le coefficient $3/2$ et ce qui est perdu avec un algorithme un peu moins puissant.

Une fois cette opération réalisée, on peut sans risques d'aliasing, transformer notre produit $\widetilde{P_N} v(x_j) w(x_j)$ dans le domaine spatial, via une FFT inverse. On se retrouve alors avec un signal sur-échantillonné (de manière artificielle), on a des $\widetilde{P_N} y(x_j)$ avec $y(x_j)=v(x_j)w(x_j)$ pour $j \in 0, \cdots ,M-1$. On transforme alors notre signal dans les domaines de Fourier puis le recompose pour dans l'intervalle $[-N/2+1,N/2]$ pour ne garder que les fréquences non artificielles.

Cette opération nous permet donc de pouvoir résoudre proprement et rapidement les problèmes non linéaires par des méthodes spectrales. Les multiples allers-retours entre domaines spatiaux et fréquentiels dûs à l'utilisation de FFT restent très compétitifs en terme de temps de calculs par rapport à une transformée de Fourier par produit matriciel.