schéma implicite

Discrétisons la même équation avec le même maillage mais utilisons cette fois une approximation à gauche pour la dérivée temporelle :

$$\frac{\partial u}{\partial t} (x_j,t_n) = \frac{u_j^{n}-u_j^{n-1}}{\Delta t}$$

Ce simple changement semble anodin. En fait les modifications engendrées sont très importantes. Observons le nouveau schéma :

$$\left\{ \begin{array}{lr} \frac{u_j^{n}-u_j^{n-1}}{\Delta t}... ...u_0^n = u_N^n = 0 & \forall n \in \mathbb{R}\end{array}\right.$$

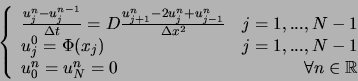
Ce schéma nécessite la résolution d'un système d'équations. Au temps $t_n$ le système d'équations s'écrit :

$$\left[ \begin{array}{ccccc} \alpha&\beta&&&\\ \beta&\alpha&... ...c{u_{N-1}^{n-1}}{\Delta t} - \beta u_0^n\\ \end{array}\right]$$

soit :

$$\left[ \begin{array}{c} u_1^n\\ u_2^n\\ \vdots\\ u_{N-2}^... ...c{u_{N-1}^{n-1}}{\Delta t} - \beta u_N^n\\ \end{array}\right]$$

avec $\alpha = - \frac{1}{\Delta t} - \frac{2D}{\Delta x^2}$ et $\beta = \frac{D}{\Delta x^2}$. Trouver les $u_j^{n}$ à partir des $u _j^{n-1}$ nécessite ici la résolution d'un système i.e. l'inversion d'une matrice. Le système est ici tridiagonal. On peut le résoudre facilement par l'algorithme de Thomas, spécialement adapté aux matrices bandes. Un tel schéma est implicite.

La discrétisation du problème induit plusieurs problématiques que nous étudions dans les sections suivantes. Nous y analyserons des problèmes de dimension 1. La valeur de $u(t^n , x_j)$ y est toujours approximée par $u_j^n$.