On peut facilement construire un schéma FTCS. Cependant, l'analyse de stabilité de Von Neumann est plus restrictive en ![]() pour
ce schéma :
pour
ce schéma :
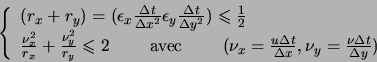
Pour
![]() et
et
![]() la première condition donne
la première condition donne
![]() ce qui est deux
fois plus sévère qu'en
ce qui est deux
fois plus sévère qu'en ![]() . De plus, les termes de dissipation artificielle sont liés au premier ordre de la dérivée
temporelle. Enfin, si le vecteur vitesse
. De plus, les termes de dissipation artificielle sont liés au premier ordre de la dérivée
temporelle. Enfin, si le vecteur vitesse ![]() est à
est à ![]() degrés par rapport à la direction des coordonnées,
il y a une très forte dissipation numérique.
degrés par rapport à la direction des coordonnées,
il y a une très forte dissipation numérique.
Il est donc important d'utiliser une bonne précision temporelle.