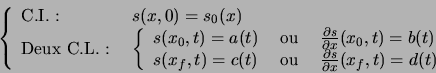Equation de transport $1D$ (linéaire)

L'équation de transport (convection-diffusion) monodimensionnelle est :

$$\frac{\partial s}{\partial t} + u \frac{\partial s}{\partial x} = \epsilon \frac{\partial^2 s}{\partial x^2}$$

Cette équation est aussi connue sous le nom de équation de Burgers Linéarisée. Le scalaire $S$ y est convecté à la vitesse $u=\textrm{const}$ et y est diffusé par le coefficient de diffusion $\epsilon$. Cette équation, qui est parabolique, peut être un modèle pour l'équation de la couche limite. Elle nécessite les mêmes C.I. et C.L. que l'équation de la chaleur, i.e. :

$$\left\{ \begin{array}{ll} \textrm{C.I. : }&s(x,0)=s_0(x)\\ ... ...artial x} (x_f,t) = d(t) \end{array}\right. \end{array}\right.$$